Example

Noun

Verb

25 + 40

addition

…

65 - 15

20 x 5

45 : 9

I have never seen the word before

I understand the word when I see or hear it

I understand the word and use it in speaking/writing

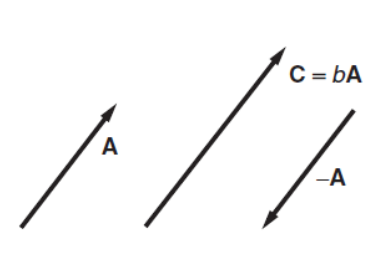
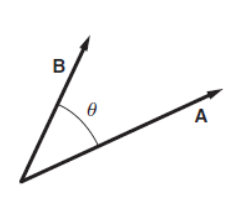
The topic of vectors provides a natural introduction to the role of mathematics in physics. By using vector notation, physical laws can often be written in compact and simple form. Modern vector notation was invented by a physicist, Willard Gibbs of Yale University, primarily to simplify the appearance of equations. For example, here is how Newton’s second law appears in nineteenth century notation:

F_x = ma_x

F_y = ma_y

F_z = ma_z.

In vector notation, one simply writes

F = ma,

where the bold face symbols F and a stand for vectors.

Mathematicians think of a vector as a set of numbers accompanied by rules for how they change when the coordinate system is changed. According to geometrical definition, a vector is a directed line segment. We can represent a vector graphically by an arrow, showing both its scale length and its direction. Vectors are sometimes labeled by letters capped by an arrow, but we shall use the convention that a bold face letter, such as A, stands for a vector.

To describe a vector we must specify both its length and its direction. If two vectors have the same length and the same direction they are equal. The vectors B and C are equal: B = C. The magnitude or size of a vector is indicated by vertical bars or, if no confusion will occur, by using italics. For example, the magnitude of A is written |A|, or simply A. If the length of A is √2, then |A| = A =√2.

Vectors can have physical dimensions, for example distance, velocity, acceleration, force, and momentum. The physical dimension of a vector is carried by its magnitude.

The Algebra of Vectors 

We will need to add, subtract, and multiply two vectors, and carry out some related operations.

If we multiply A by a simple scalar, that is, by a simple number b, the result is a new vector C = bA. If b > 0 the vector C is parallel to A, and its magnitude is b times greater. If b < 0, then C = bA is opposite in direction (antiparallel) to A, and its magnitude is C = |b| A.

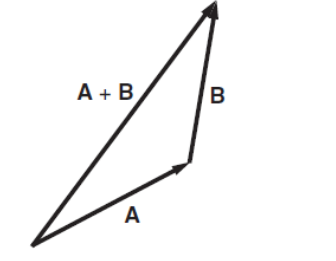
Addition of two vectors has the simple geometrical interpretation shown by the drawing. The rule is: to add B to A, place the tail of B at the head of A by parallel translation of B. The sum is a vector from the tail of A to the head of B.

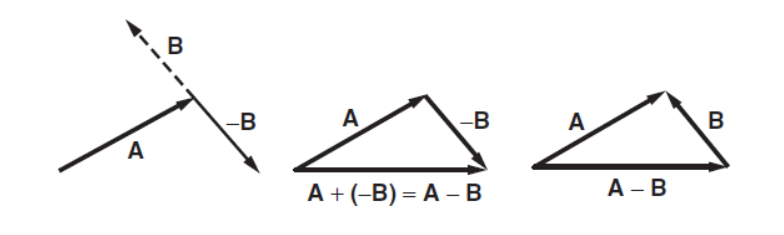
Subtracting Vectors

Because A − B = A + (−B), to subtract B from A we can simply multiply B by –1 and then add. An equivalent way to construct A − B is to place the head of B at the head of A. Then A − B extends from the tail of A to the tail of B, as shown in the drawing.

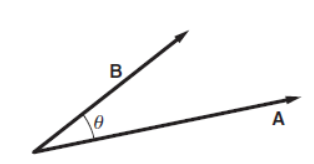
Multiplying vectors

Multiplying one vector by another could produce a vector, a scalar, or some other quantity. Two types of vector multiplication are useful in physics.

The first type of multiplication is called the scalar product because the result of the multiplication is a scalar. The scalar product is an operation that combines vectors to form a scalar. The scalar product of A and B is written as A · B, therefore often called the dot product. A · B (referred to as “A dot B”) is defined by

A · B ≡ ABcos θ.

Here θ is the angle between A and B when they are drawn tail to tail.

The second type of product useful in physics is the vector product, in which two vectors A and B are combined to form a third vector C. The symbol for vector product is a cross, so it is often called the cross product:

C = A × B.

The vector product is more complicated than the scalar product because we have to specify both the magnitude and direction of the vector A × B (called “A cross B”). The magnitude is defined as follows: if C = A × B then

C = ABsin θ

where θ is the angle between A and B when they are drawn tail to tail.

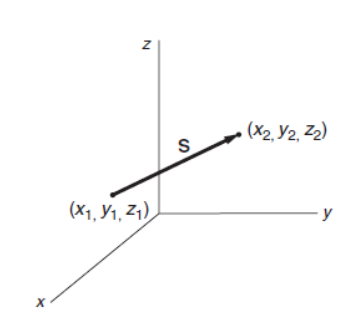
The reason for introducing vectors is that many physical quantities are conveniently described by vectors, among them velocity, force, momentum, and gravitational and electric fields.

Position and displacement

To locate the position of a point in space, we start by setting up a coordinate system. For convenience we choose a three-dimensional Cartesian system with axes x, y, and z, as shown. In order to measure position, the axes must be marked in some convenient unit of length—meters, for instance. The position of the point of interest is given by listing the values of its three coordinates, x, y, z, which we can write compactly as a position vector r(x, y, z). If we move from the point x₁, y₁, z₁ to some new position, x₂, y₂, z₂, then the displacement defines a true vector S with coordinates S x = x2 −x1, S y = y2 − y1, S z = z2 − z1. S is a vector from the initial position to the final position—it defines the displacement of a point of interest.

One way in which our displacement vector differs from vectors in pure mathematics is that in mathematics, vectors are usually pure quantities, with components described by simple numbers, whereas the magnitude S has the physical dimension of length associated with it.

(from  Kleppner D., Kolenkow R. An Introduction to Mechanics)